Skip to contents

Bland-Altman Method Comparison

Source: R/method-comparison.R
measure_bland_altman.Rd

Performs Bland-Altman analysis to compare two measurement methods. This calculates the mean bias, limits of agreement, and optionally tests for proportional bias.

Usage

measure_bland_altman(
  data,
  method1_col,
  method2_col,
  id_col = NULL,
  conf_level = 0.95,
  regression = c("none", "linear", "quadratic")
)

Arguments

data

A data frame containing paired measurements from both methods.

method1_col

Name of the column containing method 1 (reference) values.

method2_col

Name of the column containing method 2 (test) values.

id_col

Optional name of a column identifying paired observations.

conf_level

Confidence level for intervals. Default is 0.95.

regression

Test for proportional bias:

  • "none" (default): No regression test

  • "linear": Test for linear trend in bias

  • "quadratic": Test for quadratic trend

Value

A measure_bland_altman object containing:

  • data: Tibble with mean, difference, and LOA for each observation

  • statistics: List of summary statistics (bias, SD, LOA, CIs)

  • regression: Regression results if requested (model, p-value)

Details

Interpretation

The Bland-Altman plot shows the difference between methods against their mean. Key features:

  • Mean bias: Average difference (systematic error)

  • Limits of agreement (LOA): Range containing 95% of differences

  • Proportional bias: Trend in differences with concentration

Acceptance Criteria

Methods are typically considered interchangeable if:

  • Mean bias is clinically/analytically insignificant

  • LOA width is acceptable for the intended use

  • No significant proportional bias

See also

measure_deming_regression(), measure_passing_bablok()

Other method-comparison: measure_deming_regression(), measure_passing_bablok(), measure_proficiency_score()

Examples

# Compare two blood glucose meters
set.seed(123)
data <- data.frame(
  patient_id = 1:30,
  meter_A = rnorm(30, mean = 100, sd = 15),
  meter_B = rnorm(30, mean = 102, sd = 16)
)

ba <- measure_bland_altman(
  data,
  method1_col = "meter_A",
  method2_col = "meter_B",
  regression = "linear"
)

print(ba)
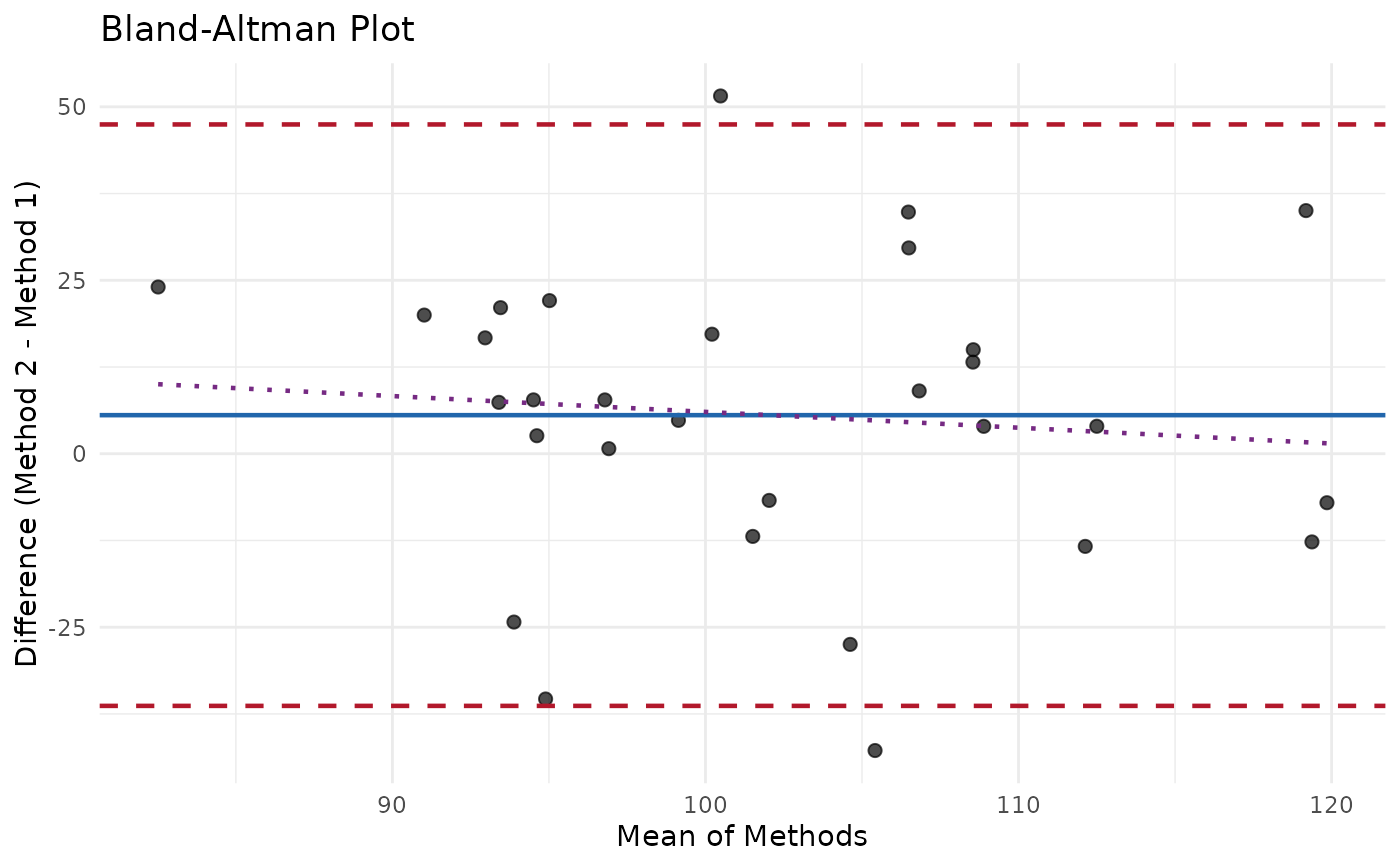
#> measure_bland_altman
#> ──────────────────────────────────────────────────────────────────────────────── 
#> 
#> Bias Statistics:
#>   n = 30 
#>   Mean bias = 5.56 
#>   SD of differences = 21.38 
#>   95% CI for bias: [-2.423, 13.54]
#> 
#> Limits of Agreement:
#>   Lower LOA = -36.34 (95% CI: [ -50.17 ,  -22.51 ])
#>   Upper LOA = 47.46 (95% CI: [ 33.63 ,  61.29 ])
#>   LOA Width = 83.8 
#> 
#> Proportional Bias Test:
#>   Slope = -0.2281 
#>   p-value = 0.6087 
#>   Result: No significant proportional bias
tidy(ba)
#> # A tibble: 8 × 2
#>   statistic      value
#>   <chr>          <dbl>
#> 1 n              30   
#> 2 mean_bias       5.56
#> 3 sd_diff        21.4 
#> 4 lower_loa     -36.3 
#> 5 upper_loa      47.5 
#> 6 loa_width      83.8 
#> 7 bias_ci_lower  -2.42
#> 8 bias_ci_upper  13.5 

# Visualize
ggplot2::autoplot(ba)
#> `geom_smooth()` using formula = 'y ~ x'